Leerfahrt

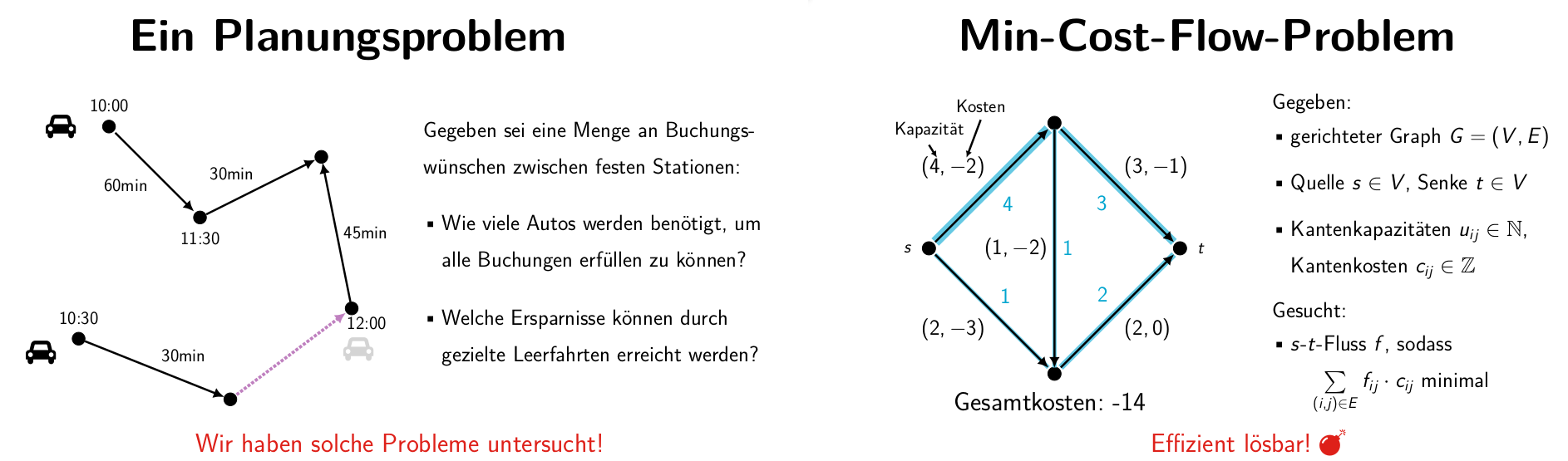
Das oben beschriebene Planungsproblem lässt sich in ein Min-Cost-Flow-Problem umwandeln. Somit ist es z.B. mit einem Netzwerk-Simplex-Algorithmus lösbar. Auf Wegen im Netzwerk-Graphen kann man an den jeweiligen Stationen warten. Solch ein Weg führt von der Quelle zur Senke. Er ist kostenlos mit unbegrenzter Kapazität. Jede Buchung besteht aus Zeit und Ort von Abfahrt und Ankunft. Sie wird zu einer Kante im Netzwerk des Min-Cost-Flow-Problems. Diese hat eine Kapazität von 1 und einen Kostenwert von -1, also Profit 1. Über die Kapazität der Quellkanten lässt sich eine initiale Verteilung der Autos auf die Stationen einstellen. 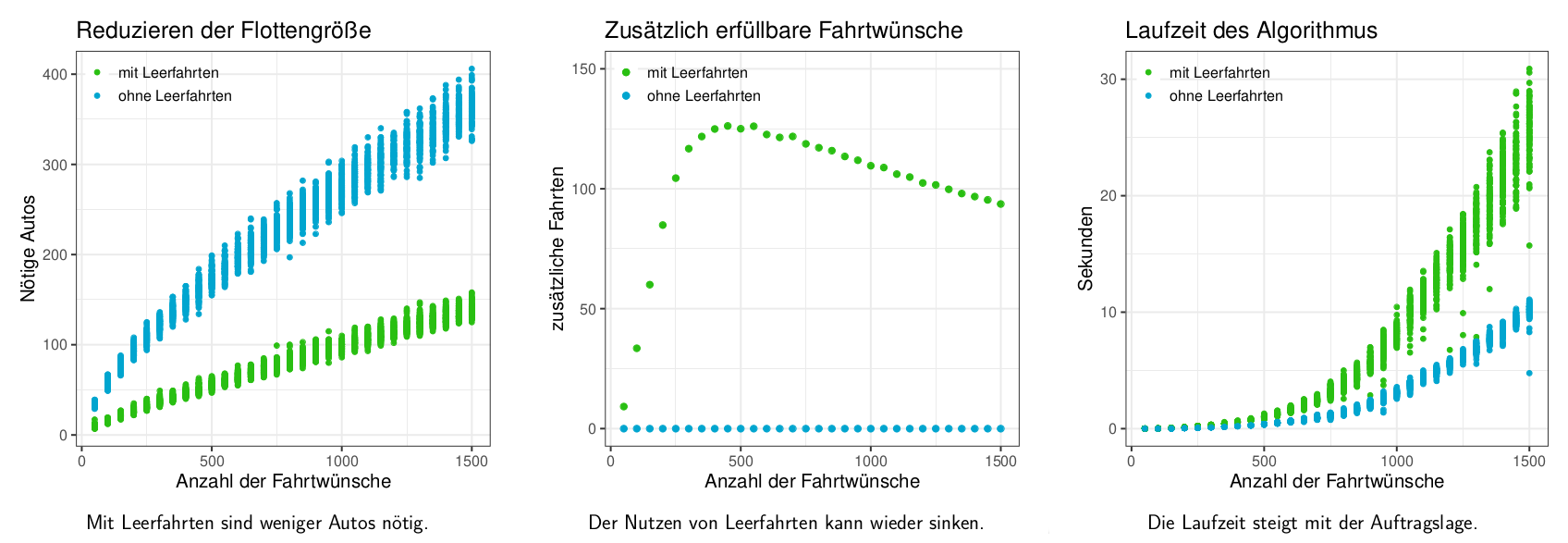Manchmal fehlt für die Erfüllung eines Auftrags ein Auto. Aber eine rechtzeitige Leerfahrt könnte ein Auto zum Abfahrtsort transportieren. Wir berücksichtigen Leerfahrten bei der Planung. Dazu fügen wir machbare Leerfahrtskanten mit Leerfahrtskosten zu allen Abfahrtsknoten hinzu. Beim Prüfen der zeitlichen Durchführbarkeit dieser Leerfahrten beachten wir die Distanz zwischen den Stationen.

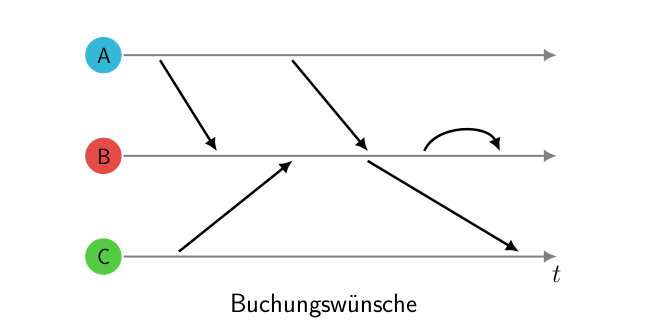
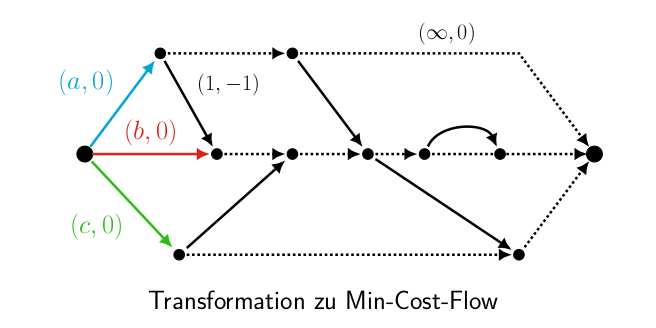
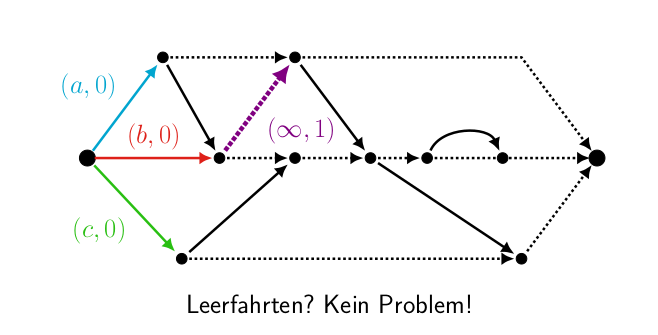
Durch das Anpassen der Kantenkosten und Kantenkapazitäten lassen sich unterschiedliche Optimierungsziele definieren. Hierdurch lassen sich dann einige interessante Fragen beantworten:

• Maximal erfüllbare Aufträge bei fester Anzahl Autos?
• Welche Leerfahrten für maximalen Profit?
• Wie viel Gewinn erhält man durch Zunahme eines Autos?
• Lohnt sich das Nutzen von Leerfahrten?

Im Rahmen einer “Computational Study” wurde diese Reduktion in einer Java-Anwendung implementiert und das Min-Cost-Flow-Problem mittels eines Netzwerk-Simplex-Algorithmus gelöst.